1> A figura 10-31a mostra um disco que pode girar em torno de um eixo perpendicular à sua face a uma distância h do centro do disco. A figura 10-31b mostra o momento de inércia I do disco em relação ao eixo em função da distância h, do centro até a borda do disco. A escala do eixo I é definida por I(A) = 0,050 kg . mˆ2 e I (B) = 0,150 kg . mˆ2. Qual é a massa do disco?
2> Calcule o momento de inércia de uma régua de um metro, com uma massa de 0,56 kg, em relação a um eixo perpendicular à régua na marca de 20 cm. (Trate a régua como uma barra fina.)
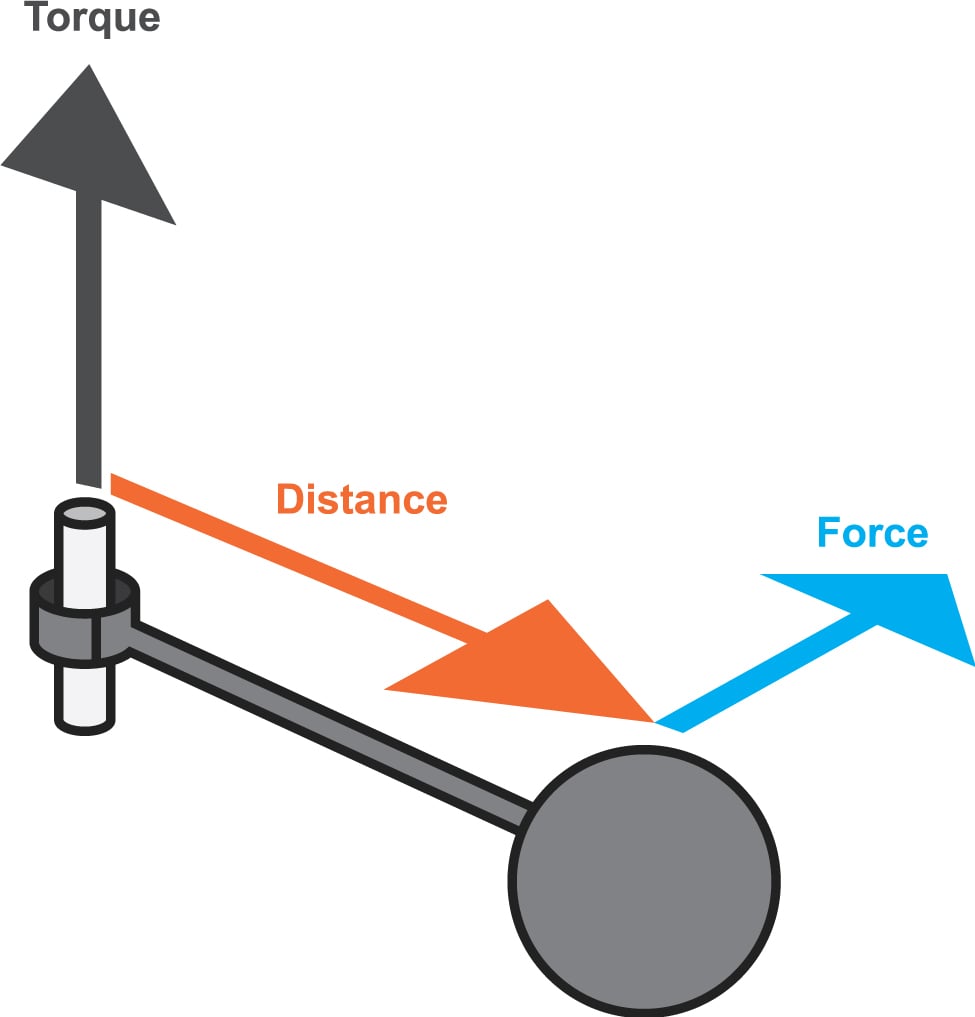
3> O corpo da figura 10-36 pode girar em torno de um eixo perpendicular ao papel passando por O e está submetido a duas forças, como mostra a figura. Se r1 = 1,30 m, r2 = 2,15 m, F1 = 4,20 N, F2 = 4,90 N, teta1 = 75,0º e teta2 = 60,0º, qual é o torque resultante em relação ao eixo?
4> Uma pequena bola de massa 0,75 kg está presa a uma das extremidades de uma barra de 1,25 m de comprimento e massa desprezível. A outra extremidade da barra está pendurada em um eixo. Qual é o módulo do torque exercido pela força gravitacional em relação ao eixo quando o pêndulo assim formado faz um ângulo de 30º com a vertical?
5> Se um torque de 32,0 N.m exercido sobre uma roda produz uma aceleração angular de 25,0 rad/sˆ2, qual é o momento de inércia da roda?
6> Na figura, o bloco 1 tem massa m1 = 460g, o bloco 2 tem massa m2 = 500g, e a polia, que está montada em um eixo horizontal com atrito desprezível, tem um raio R = 5,00 cm. Quando o sistema é liberado a partir do repouso, o bloco 2 cai 75,0 cm em 5,00 sem que a corda deslize na borda da polia. (a) Qual é o módulo da aceleração dos blocos? (b) Qual é o valor da Tensão T2 e (c) da Tensão T1? (d) Qual é o módulo da aceleração angular da polia? (e) Qual é o momento de inércia da polia?