Aula de Hoje - 08/setembro

Link da Aula

Determinação da aceleração da gravidade local

Resumindo a Primeira Aula

Grandeza Angular

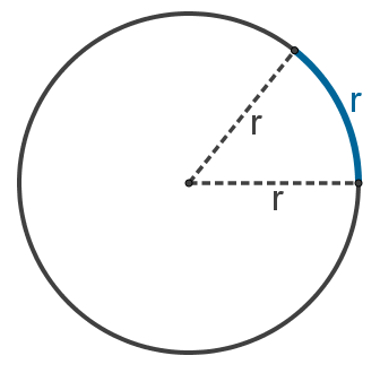
1> Radiano é o arco cujo comprimento é igual ao tamanho de um raio.

2> Grandezas Angulares:

3> Período e Frequência:

4> Logo para transformarmos as grandezas escalares em grandezas angulares, basta dividirmos pelo Raio (R). Neste caso temos uma nova Cinemática Angular.

5> Movimento Circular Uniforme

Aula 3 - Exercícios de Sala

1> O corpo da figura 10-36 pode girar em torno de um eixo perpendicular ao papel passando por O e está submetido a duas forças, como mostra a figura. Se r1 = 1,30 m, r2 = 2,15 m, F1 = 4,20 N, F2 = 4,90 N, teta1 = 75,0º e teta2 = 60,0º, qual é o torque resultante em relação ao eixo?

2> Uma pequena bola de massa 0,75 kg está presa a uma das extremidades de uma barra de 1,25 m de comprimento e massa desprezível. A outra extremidade da barra está pendurada em um eixo. Qual é o módulo do torque exercido pela força gravitacional em relação ao eixo quando o pêndulo assim formado faz um ângulo de 30º com a vertical?

3> Se um torque de 32,0 N.m exercido sobre uma roda produz uma aceleração angular de 25,0 rad/sˆ2, qual é o momento de inércia da roda?

4> Na figura, o bloco 1 tem massa m1 = 460g, o bloco 2 tem massa m2 = 500g, e a polia, que está montada em um eixo horizontal com atrito desprezível, tem um raio R = 5,00 cm. Quando o sistema é liberado a partir do repouso, o bloco 2 cai 75,0 cm em 5,00 sem que a corda deslize na borda da polia. (a) Qual é o módulo da aceleração dos blocos? (b) Qual é o valor da Tensão T2 e (c) da Tensão T1? (d) Qual é o módulo da aceleração angular da polia? (e) Qual é o momento de inércia da polia?

Aula 3 - Dinâmica de Rotação

Falaremos do Teorema dos Eixos Paralelos. Teorema que nos mostra como calcular o Momento de Inércia em um eixo paralelo ao Centro de Massa:

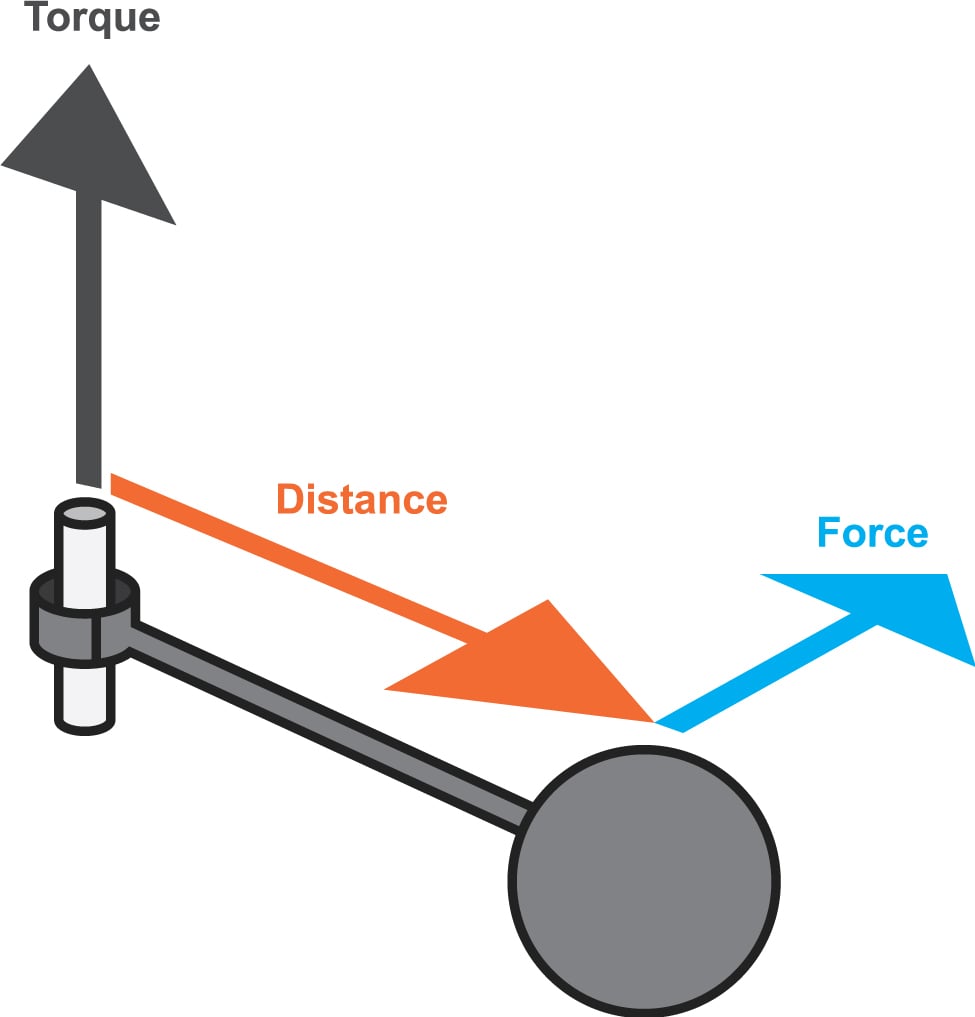
Em nossa 3ª aula, passaremos a falar do conceito de Momento de uma Força - Torque. Faremos a relação do conceito com o que aprendemos anteriormente.

Vídeo Introdutório para entendermos Torque

Aula sobre Torque na Unicamp

No final da aula iremos discutir sobre Equilíbrio de Rotação dos Corpos Rígidos. Estaremos discutindo problemas como:

Explicando Torque e Dinâmica de Rotação

Universo Mecânico:

Faremos nosso primeiro Laboratório Virtual:

Determinação da aceleração da gravidade local

Roteiro

Faremos, também, mais um exercício valendo pontos.

Aula 2 - Exercícios de Sala

1> Calcule o momento de inércia de uma roda que possui uma energia cinética de 24 400 J quando gira 602 rev/min.

2> A figura 10-31a mostra um disco que pode girar em torno de um eixo perpendicular à sua face a uma distância h do centro do disco. A figura 10-31b mostra o momento de inércia I do disco em relação ao eixo em função da distância h, do centro até a borda do disco. A escala do eixo I é definida por I(A) = 0,050 kg . mˆ2 e I (B) = 0,150 kg . mˆ2. Qual é a massa do disco?

3> Calcule o momento de inércia de uma régua de um metro, com uma massa de 0,56 kg, em relação a um eixo perpendicular à régua na marca de 20 cm. (Trate a régua como uma barra fina.)

Aula 2 - Energia Cinética de Rotação e Momento de Inércia

Link para aula de hoje

Em nossa 2ª aula faremos um exercício dobre a aula passada - Movimento Circular.

Após isso definiremos a energia cinética de rotação e introduziremos o conceito de Momento de Inércia.

Momento de Inércia de alguns Sólidos

Falaremos, também, do Teorema dos Eixos Paralelos. Teorema que nos mostra como calcular o Momento de Inércia em um eixo paralelo ao Centro de Massa:

Aula da Unicamp de Cinemática de Rotação

Simulador Phet

https://phet.colorado.edu/pt_BR/simulation/legacy/rotation

Outros Simuladores:

http://plato.if.usp.br/2-2003/fap0153d/applets/rotacoes.html

Importante: Teremos exercício durante a aula valendo Pontos.

Exercícios da Aula 1

1> Qual é a velocidade angular (a) do ponteiro dos segundos, (b) do ponteiro de minutos e (c) do ponteiro de horas de um relógio analógico? Dê as respostas em radianos por segundo.

2> A posição angular de um ponto de uma roda é dado por: teta = 2 + 4tˆ2 + 3tˆ3, onde teta está em radianos e t em segundos. Em t = 0, qual é (a) a posição e (b) a velocidade angular do ponto? (c) Qual é a velocidade angular em t = 4s? (d) Calcule a aceleração angular em t = 2 s. (e) A aceleração angular da roda é constante?

3> Um disco, inicialmente girando a 120 rad/s, é freado com uma aceleração angular constante de módulo 4 rad/sˆ2. (a) Quanto tempo o disco leva para parar? (b) Qual é o ângulo total descrito pelo disco durante esse tempo?

4> Calcule o momento de inércia de uma roda que possui uma energia cinética de 24 400 J quando gira 602 rev/min.