Aula 5 - Exercícios de Sala

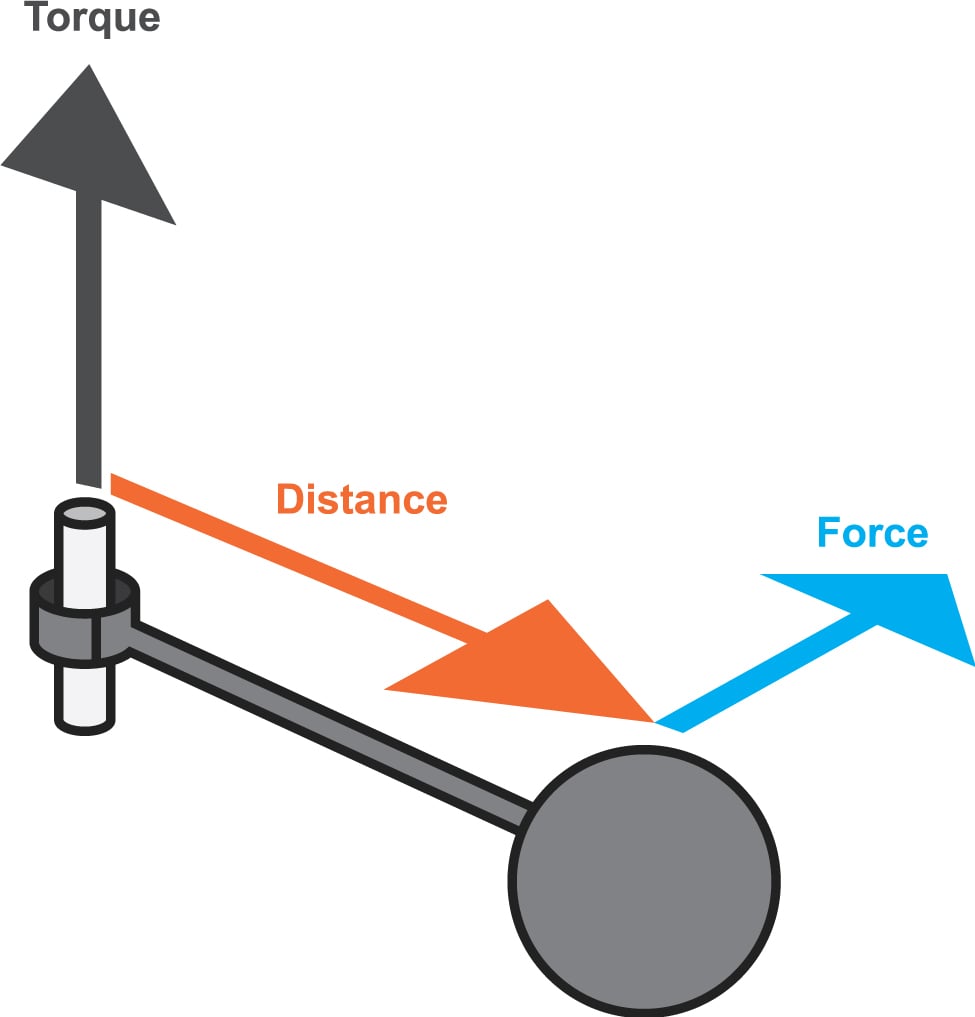
1> Em termos dos vetores unitários, qual é o torque resultante em relação à origem a que está submetida uma pulga localizada nas coordenadas (0; -4,0 m; 5,0 m) quando as forças F1 = 3 k (N) e F2 = - 2 j (N) agem sobre a pulga?

2> Em um certo instante, a força F = 4,0 j (N) age sobre um objeto de 0,25 kg cujo vetor posição é r = (2,0 i - 2,0 k)  m e cujo vetor velocidade é v = (-5,0 i + 5,0 k) m/s. Em relação à origem e em termos dos vetores unitários, qual é (a) o momento angular do objeto e (b) o torque que age sobre o objeto?

3> Um objeto de 2,0 kg, que se comporta como uma partícula se move em um plano com componentes de velocidade vx = 30 m/s e vy = 60 m/s ao passar por um ponto de coordenadas (3,0; -4,0)m. Nesse instante, em termos dos vetores unitários, qual é o momento angular do objeto em relação (a) à origem e (b) ao ponto (-2,0; -2,0) m?

Aula 5 - Momento Angular

Caros alunos, peço por favor, que coloquem o nome, curso e unidade (cidade) no comentário deste post para que eu possa saber quais alunos assistiram a aula. Agradeço a atenção.


Em nossa aula 5 o assunto principal é o Momento Angular. Momento Angular é uma grandeza similar ao momento linear para o mundo das rotações.

Para entender essas grandezas é necessário recorda o produto vetorial

Produto Vetorial:

Regra da Mão Direita:

Exemplo de Produto Vetorial

Discutindo de forma rápida as grandezas Vetor Torque e Momento Angular:

Momento Angular - Universo Mecânico

Aula sobre Momento Angular na Unicamp:

Harmonia dos Mundos - Cosmos

Lendo Sobre Kepler

Importante

Caros alunos neste momento difícil que todos nós passamos é de extrema importância que primeiramente se cuidem. Além disso para o seguimento do curso é fundamental que desenvolvam as atividades do AVA - Unidade I e Unidade II. Continuem acompanhando as aulas no AVA e aqui no Blog. 

Qualquer dúvida: ruvlemes@anhanguera.com

Regras do Carrinho de Ratoeira - Relatório

Regras – Carrinho com Ratoeira

1> A equipe deverá ser formada de até 4 elementos.

2> Construa um veículo que se desloque o mais rápido possível uma distância de 5 m, quando a mola da ratoeira é liberada.

3> A ratoeira deve ser parte do carro e mover-se junto com ele.

4> Você poderá usar apenas uma ratoeira.

5> Nenhum outro meio de propulsão é permitido.

6> A competição ocorrerá como corrida de arrancada. Termos duas pistas de 5 m por 90 cm.

7> Para liberação do carrinho na largada, você deverá ter um sistema remoto. Você não poderá ter contato físico direto com a ratoeira (pode ser um bastão para tocar na mesma).

8> No caso de o carrinho queimar a linha demarcatória da pista ele será desclassificado naquele ponto. Caso os dois queimem, vence o carrinho que queimou mais próximo da linha de chegada.

9> Chassis, rodas e eixos, podem ser feitos de qualquer tipo de material, desde que não sejam perigosos.

10> A ratoeira deverá ter no máximo (base) 12cm x 7 cm. A haste de liberação e o engate não poderão ser modificados.

11> Casos omissos nas regras serão decididos pela comissão julgadora. A comissão julgadora é o professor.

RELATÓRIO

1> Nome dos Elementos do Grupo

2> Projeto (dimensões – Foto ou desenho)

3> Física da disciplina envolvida no projeto – Relação

4> Problemas e Soluções

5> Conclusão

6> Referências

Exercícios de Sala - Aula 4

1> O corpo da figura 10-36 pode girar em torno de um eixo perpendicular ao papel passando por O e está submetido a duas forças, como mostra a figura. Se r1 = 1,30 m, r2 = 2,15 m, F1 = 4,20 N, F2 = 4,90 N, teta1 = 75,0º e teta2 = 60,0º, qual é o torque resultante em relação ao eixo?

2> Uma pequena bola de massa 0,75 kg está presa a uma das extremidades de uma barra de 1,25 m de comprimento e massa desprezível. A outra extremidade da barra está pendurada em um eixo. Qual é o módulo do torque exercido pela força gravitacional em relação ao eixo quando o pêndulo assim formado faz um ângulo de 30º com a vertical?

3> Se um torque de 32,0 N.m exercido sobre uma roda produz uma aceleração angular de 25,0 rad/sˆ2, qual é o momento de inércia da roda?

4> Na figura, o bloco 1 tem massa m1 = 460g, o bloco 2 tem massa m2 = 500g, e a polia, que está montada em um eixo horizontal com atrito desprezível, tem um raio R = 5,00 cm. Quando o sistema é liberado a partir do repouso, o bloco 2 cai 75,0 cm em 5,00 sem que a corda deslize na borda da polia. (a) Qual é o módulo da aceleração dos blocos? (b) Qual é o valor da Tensão T2 e (c) da Tensão T1? (d) Qual é o módulo da aceleração angular da polia? (e) Qual é o momento de inércia da polia?

Aula 4 - Dinâmica de Rotação

Falaremos do Teorema dos Eixos Paralelos. Teorema que nos mostra como calcular o Momento de Inércia em um eixo paralelo ao Centro de Massa:

Em nossa 4ª aula, passaremos a falar do conceito de Momento de uma Força - Torque. Faremos a relação do conceito com o que aprendemos anteriormente.

Vídeo Introdutório para entendermos Torque

Aula sobre Torque na Unicamp

No final da aula iremos discutir sobre Equilíbrio de Rotação dos Corpos Rígidos. Estaremos discutindo problemas como:

Explicando Torque e Dinâmica de Rotação

Universo Mecânico:

Aula 3 - Laboratório - Determinação da Aceleração da Gravidade Local e Centro de Massa

Pindamonhangaba - 11/03

Taubaté - 16/03

Utilização do Pêndulo Simples para determinação da Aceleração da Gravidade Local:

Determinação do Período de Oscilação de um pêndulo simples:

Isolar g, medir L e T e determinar a aceleração da gravidade local. Repetir o procedimento três vezes com tamanhos diferentes de pêndulos.

A 2ª parte do laboratório é fazendo uso do centro de equilíbrio determinar o centro de massa de algumas figuras geométricas conhecidas.

Roteiro - Taubaté

Roteiro - Pinda