Aula 5 - Exercícios de Sala

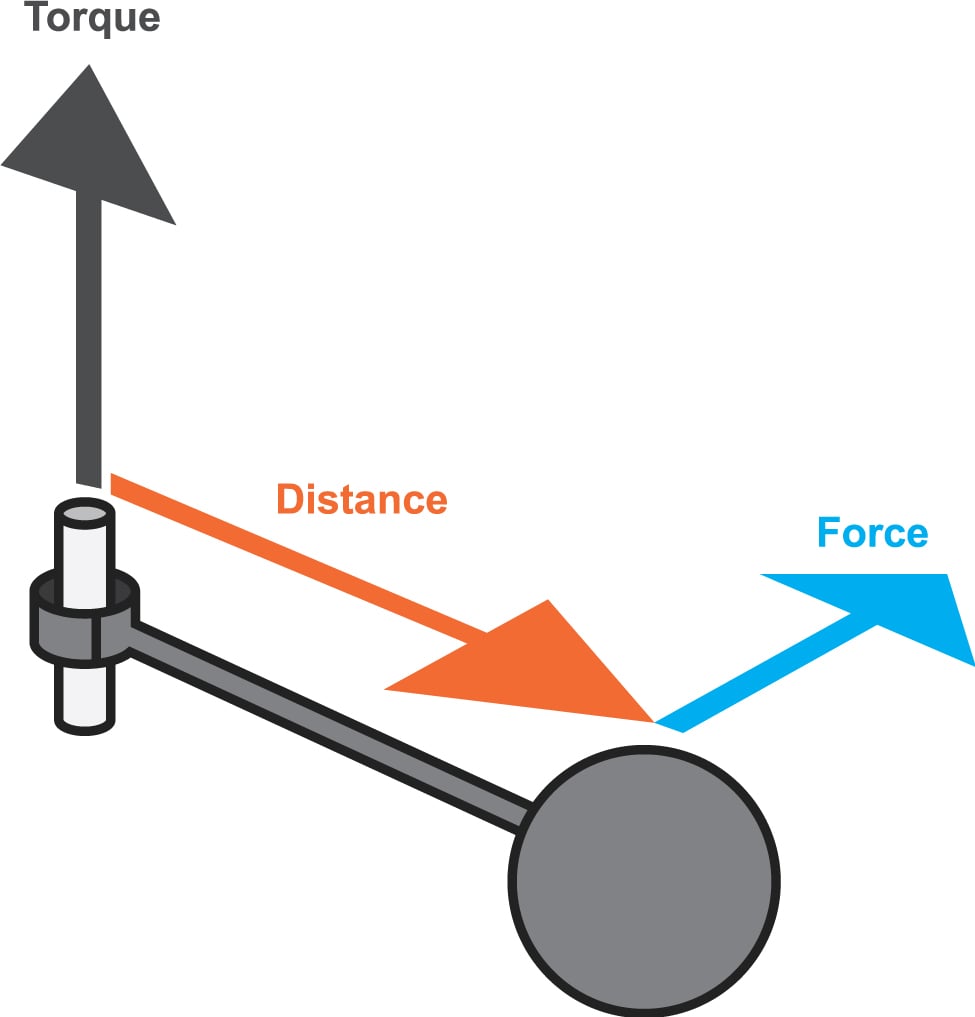
1> Em termos dos vetores unitários, qual é o torque resultante em relação à origem a que está submetida uma pulga localizada nas coordenadas (0; -4,0 m; 5,0 m) quando as forças F1 = 3 k (N) e F2 = - 2 j (N) agem sobre a pulga?

2> Em um certo instante, a força F = 4,0 j (N) age sobre um objeto de 0,25 kg cujo vetor posição é r = (2,0 i - 2,0 k)  m e cujo vetor velocidade é v = (-5,0 i + 5,0 k) m/s. Em relação à origem e em termos dos vetores unitários, qual é (a) o momento angular do objeto e (b) o torque que age sobre o objeto?

3> Uma partícula sofre ação de dois torques em relação à origem: Torque 1 tem módulo de 2,0 N.m e aponta no sentido positivo do eixo x; Torque 2 tem módulo de 4,0 N.m e aponta no sentido negativo do eixo y. Determine dL/dt, onde L é o momento angular da partícula em relação à origem, em termos dos vetores unitários.

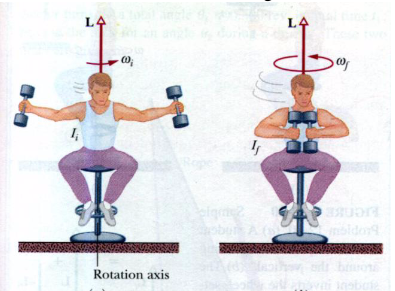
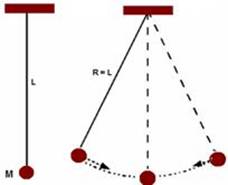
4> Duas patinadoras com 50 kg de massa, que se movem com velocidade escalar de 1,4 m/s, se aproximam em trajetórias paralelas separadas por 3,0 m. Uma das patinadoras carrega uma vara comprida, de massa desprezível, segurando-a em uma extremidade, e a outra se agarra à outra extremidade ao passar pela vara, o que faz com que as patinadoras passem a descrever uma circunferência em torno do centro da vara. Suponha que o atrito entre entre as patinadoras e o gelo é desprezível. Qual é (a) o raio da circunferência, (b) a velocidade angular das patinadoras, (c) a energia cinética do sistema das duas patinadoras? Em seguida, as patinadoras puxam a vara até ficarem separadas por uma distância de 1,0 m. Nesse instante, qual é (d) a velocidade angular das patinadoras e (e) a energia cinética do sistema? (f) De onde vem a energia cinética adicional?

5> Uma barata de massa 0,17 kg corre no sentido anti-horário na borda de um disco circular de raio 15 cm e momento de inércia 5,0 x 10ˆ-3 kg . mˆ2, montado em um eixo vertical com atrito desprezível. A velocidade da barata (em relação ao chão) é de 2,0 m/s e o disco gira no sentido horário com uma velocidade angular de 2,8 rad/s. A barata encontra uma migalha de pão na borda e, obviamente, para. Qual é a velocidade angular do disco depois que a barata para?

Aula 5 - Dinâmica de Rotação - Parte Final

Em nossa aula 5 o assunto principal é o Momento Angular. Momento Angular é uma grandeza similar ao momento linear para o mundo das rotações.

Para entender essas grandezas é necessário recordar o produto vetorial

Produto Vetorial:

Regra da Mão Direita:

Exemplo de Produto Vetorial

Discutindo de forma rápida as grandezas Vetor Torque e Momento Angular:

Momento Angular - Universo Mecânico

Aula sobre Momento Angular na Unicamp:

Falaremos, também, sobre a 2ª Lei de Newton para as rotações.

A seguir discutiremos o Princípio de Conservação do Momento Angular.

Leis de Kepler

Aula

Aula 4 - Laboratório - Determinação da Aceleração da Gravidade Local

Em nossa próxima aula terminaremos o exercício da aula anterior. Falaremos de Produto Vetorial e logo depois faremos o Laboratório. Não esqueça de imprimir o Roteiro (1 por grupo).

Utilização do Pêndulo Simples para determinação da Aceleração da Gravidade Local:

Determinação do Período de Oscilação de um pêndulo simples:

Isolar g, medir L e T e determinar a aceleração da gravidade local. Repetir o procedimento três vezes com tamanhos diferentes de pêndulos.

Imprimir Roteiro e levar para o Laboratório (1 por grupo)

Roteiro - Taubaté

Demonstração

Aula 3 - Exercícios de Sala

 1> A figura 10-31a mostra um disco que pode girar em torno de um eixo perpendicular à sua face a uma distância h do centro do disco. A figura 10-31b mostra o momento de inércia I do disco em relação ao eixo em função da distância h, do centro até a borda do disco. A escala do eixo I é definida por I(A) = 0,050 kg . mˆ2 e I (B) = 0,150 kg . mˆ2. Qual é a massa do disco?

2> Calcule o momento de inércia de uma régua de um metro, com uma massa de 0,56 kg, em relação a um eixo perpendicular à régua na marca de 20 cm. (Trate a régua como uma barra fina.) 

3> O corpo da figura 10-36 pode girar em torno de um eixo perpendicular ao papel passando por O e está submetido a duas forças, como mostra a figura. Se r1 = 1,30 m, r2 = 2,15 m, F1 = 4,20 N, F2 = 4,90 N, teta1 = 75,0º e teta2 = 60,0º, qual é o torque resultante em relação ao eixo?

4> Uma pequena bola de massa 0,75 kg está presa a uma das extremidades de uma barra de 1,25 m de comprimento e massa desprezível. A outra extremidade da barra está pendurada em um eixo. Qual é o módulo do torque exercido pela força gravitacional em relação ao eixo quando o pêndulo assim formado faz um ângulo de 30º com a vertical?

5> Se um torque de 32,0 N.m exercido sobre uma roda produz uma aceleração angular de 25,0 rad/sˆ2, qual é o momento de inércia da roda?

6> Na figura, o bloco 1 tem massa m1 = 460g, o bloco 2 tem massa m2 = 500g, e a polia, que está montada em um eixo horizontal com atrito desprezível, tem um raio R = 5,00 cm. Quando o sistema é liberado a partir do repouso, o bloco 2 cai 75,0 cm em 5,00 sem que a corda deslize na borda da polia. (a) Qual é o módulo da aceleração dos blocos? (b) Qual é o valor da Tensão T2 e (c) da Tensão T1? (d) Qual é o módulo da aceleração angular da polia? (e) Qual é o momento de inércia da polia?

Aula 3 - Dinâmica de Rotação

Aula 3 

Falaremos do Teorema dos Eixos Paralelos. Teorema que nos mostra como calcular o Momento de Inércia em um eixo paralelo ao Centro de Massa:

Em nossa 3ª aula, passaremos a falar do conceito de Momento de uma Força - Torque. Faremos a relação do conceito com o que aprendemos anteriormente.

Vídeo Introdutório para entendermos Torque

Aula sobre Torque na Unicamp

No final da aula iremos discutir sobre Equilíbrio de Rotação dos Corpos Rígidos. Estaremos discutindo problemas como:

Explicando Torque e Dinâmica de Rotação

Universo Mecânico:

Datas Importantes

 Abaixo você encontra datas importantes do 1º Bimestre:

26/Agosto - Laboratório

09/Setembro - Competição - Carrinho com Ratoeira

23/Setembro - Prova B1

Iniciação Tecnológica - Guindaste Hidráulico

https://www.youtube.com/watch?v=sft0OzAC8gw

Regras

Materiais Para Construção

Utilização de Madeira, Canos, Plásticos, dobradiças, materiais leves.

Seringas: quantidade sem limites, usar seringas de até 20 ml.

Objetivo: Posicionar o Guindaste em sua posição inicial. Buscar um objeto a 90º da posição inicial, levantar o objeto e trazer em direção a linha inicial. Levar o objeto a 90º ao contrário do movimento inicial. Abaixar o objeto e liberá-lo do guindaste.

Quem vence?

A equipe que tiver o maior fator.

O fator será calculado pela divisão da massa levantada e o tempo para completar o movimento.

Grupos:

Até 4 Pessoas.

Tamanho Máximo:

Altura não poderá ultrapassar 50 cm.

A Base não poderá ultrapassar as dimensões: 50 cm x 50 cm.

A competição:

Cada Guindaste terá 2 oportunidades para obter seu fator. Ficará valendo o fator maior.

Os quatro melhores serão classificados para a fase final, onde o grupo deverá levantar a massa que suportar, fazendo o mesmo movimento, mas abaixando o peso em pontos a serem definidos pelo professor. Novamente os grupos terão duas chances. No caso de nenhum grupo efetuar a proposta pedida na segunda fase, valerão os resultados da primeira fase.

Problemas: Qualquer item não esclarecido pela regra terá como fator de decisão o prof. Maurício Ruv Lemes.

OBS: Se o guindaste apresentar vazamento estará desclassificado.

RELATÓRIO

O Relatório deve ter os seguintes itens:

1>  Projeto

2> Procedimento de Construção (Descrição do Projeto)

3> Problemas e Soluções

4> Física do Projeto

5> Conclusão

6> Referências

Aula 2 - Exercícios de Sala

1> Qual é a velocidade angular (a) do ponteiro dos segundos, (b) do ponteiro de minutos e (c) do ponteiro de horas de um relógio analógico? Dê as respostas em radianos por segundo.

2> Um disco, inicialmente girando a 120 rad/s, é freado com uma aceleração angular constante de módulo 4 rad/sˆ2. (a) Quanto tempo o disco leva para parar? (b) Qual é o ângulo total descrito pelo disco durante esse tempo?

3> Calcule o momento de inércia de uma roda que possui uma energia cinética de 24 400 J quando gira 602 rev/min.

4> A figura 10-31a mostra um disco que pode girar em torno de um eixo perpendicular à sua face a uma distância h do centro do disco. A figura 10-31b mostra o momento de inércia I do disco em relação ao eixo em função da distância h, do centro até a borda do disco. A escala do eixo I é definida por I(A) = 0,050 kg . mˆ2 e I (B) = 0,150 kg . mˆ2. Qual é a massa do disco?

5> Calcule o momento de inércia de uma régua de um metro, com uma massa de 0,56 kg, em relação a um eixo perpendicular à régua na marca de 20 cm. (Trate a régua como uma barra fina.)

Aula 2 - Energia Cinética de Rotação e Momento de Inércia

 Aula 2:

 

Iniciaremos terminando Movimento Angular e Cinemática Angular.

Após isso definiremos a energia cinética de rotação e introduziremos o conceito de Momento de Inércia.

Momento de Inércia de alguns Sólidos

Falaremos, também, do Teorema dos Eixos Paralelos. Teorema que nos mostra como calcular o Momento de Inércia em um eixo paralelo ao Centro de Massa:

Aula da Unicamp de Cinemática de Rotação

Simulador Phet

https://phet.colorado.edu/pt_BR/simulation/legacy/rotation

Outros Simuladores:

http://plato.if.usp.br/2-2003/fap0153d/applets/rotacoes.html

Ponte de Takoma:

https://www.youtube.com/watch?v=j-zczJXSxnw

Carrinho com Ratoeira

Regras – Carrinho com Ratoeira

1> A equipe deverá ser formada de até 3 elementos.

2> Construa um veículo que se desloque o mais rápido possível uma distância de 3 m, quando a mola da ratoeira é liberada.

3> A ratoeira deve ser parte do carro e mover-se junto com ele.

4> Você poderá usar apenas uma ratoeira.

5> Nenhum outro meio de propulsão é permitido.

6> A competição ocorrerá como corrida de arrancada. Teremos duas pistas de 3 m por 90 cm.

7> Para liberação do carrinho na largada, você deverá ter um sistema remoto. Você não poderá ter contato físico direto com a ratoeira (pode ser um bastão para tocar na mesma).

8> No caso de o carrinho queimar a linha demarcatória da pista ele será desclassificado naquele ponto. Caso os dois queimem, vence o carrinho que queimou mais próximo da linha de chegada.

9> Chassis, rodas e eixos, podem ser feitos de qualquer tipo de material, desde que não sejam perigosos.

10> A ratoeira deverá ter no máximo (base) 12 cm x 7 cm. A haste de liberação e o engate não poderão ser modificados.

11> Casos omissos nas regras serão decididos pela comissão julgadora. A comissão julgadora é o professor.

RELATÓRIO

1> Nome dos Elementos do Grupo

2> Projeto (dimensões – Foto ou desenho)

3> Física da disciplina envolvida no projeto – Relação

4> Problemas e Soluções

5> Conclusão

6> Referências

Aula 1 - Exercícios de Sala

1> Qual é a velocidade angular (a) do ponteiro dos segundos, (b) do ponteiro de minutos e (c) do ponteiro de horas de um relógio analógico? Dê as respostas em radianos por segundo.

2> A posição angular de um ponto de uma roda é dado por: teta = 2 + 4tˆ2 + 3tˆ3, onde teta está em radianos e t em segundos. Em t = 0, qual é (a) a posição e (b) a velocidade angular do ponto? (c) Qual é a velocidade angular em t = 4s? (d) Calcule a aceleração angular em t = 2 s. (e) A aceleração angular da roda é constante?

3> Um disco, inicialmente girando a 120 rad/s, é freado com uma aceleração angular constante de módulo 4 rad/sˆ2. (a) Quanto tempo o disco leva para parar? (b) Qual é o ângulo total descrito pelo disco durante esse tempo?

Aula 1 - Iniciando o Curso

Em nossa primeira aula explicaremos o PEA, falaremos dos critérios de avaliação e como será nosso 2º Semestre.

Meu email:
ruvlemes@anhanguera.com

O que estudaremos em Física Geral Experimental: Energia ?

• Rotação dos Corpos Rígidos
• Dinâmica do Movimento de Rotação
• Mecânica dos Fluidos
• Temperatura e Calor

Em nossa primeira aula iniciaremos falando sobre grandezas angulares: posição angular, velocidade angular, aceleração angular. Relacionaremos as grandezas escalares com as grandezas angulares. Introduziremos o conceito de Movimento Circular Uniforme, suas equações e possíveis generalizações.

Movimento Circular

Ponte de Takoma

Aula 1