Carrinho com Ratoeira - Resultados

 Resultados:

Campeão

2º Lugar

3º Lugar

4º Lugar

Disputas

Aula 6 - Iniciação Tecnológica do Carrinho com Ratoeira

Regras – Carrinho com Ratoeira

1> A equipe deverá ser formada de até 4 elementos.

2> Construa um veículo que se desloque o mais rápido possível uma distância de 3 m, quando a mola da ratoeira é liberada.

3> A ratoeira deve ser parte do carro e mover-se junto com ele.

4> Você poderá usar apenas uma ratoeira.

5> Nenhum outro meio de propulsão é permitido.

6> A competição ocorrerá como corrida de arrancada. Teremos duas pistas de 3 m por 90 cm.

7> Para liberação do carrinho na largada, você deverá ter um sistema remoto. Você não poderá ter contato físico direto com a ratoeira (pode ser um bastão para tocar na mesma).

8> No caso de o carrinho queimar a linha demarcatória da pista ele será desclassificado naquele ponto. Caso os dois queimem, vence o carrinho que queimou mais próximo da linha de chegada.

9> Chassis, rodas e eixos, podem ser feitos de qualquer tipo de material, desde que não sejam perigosos.

10> A ratoeira deverá ter no máximo (base) 12cm x 7 cm. A haste de liberação e o engate não poderão ser modificados.

11> Casos omissos nas regras serão decididos pela comissão julgadora. A comissão julgadora é o professor.

RELATÓRIO

1> Nome dos Elementos do Grupo

2> Projeto (dimensões – Foto ou desenho)

3> Física da disciplina envolvida no projeto – Relação

4> Problemas e Soluções

5> Conclusão

6> Referências

Aula 5 - Exercícios de Sala

1> Em termos dos vetores unitários, qual é o torque resultante em relação à origem a que está submetida uma pulga localizada nas coordenadas (0; -4,0 m; 5,0 m) quando as forças F1 = 3 k (N) e F2 = - 2 j (N) agem sobre a pulga?

2> Em um certo instante, a força F = 4,0 j (N) age sobre um objeto de 0,25 kg cujo vetor posição é r = (2,0 i - 2,0 k)  m e cujo vetor velocidade é v = (-5,0 i + 5,0 k) m/s. Em relação à origem e em termos dos vetores unitários, qual é (a) o momento angular do objeto e (b) o torque que age sobre o objeto?

3> Uma partícula sofre ação de dois torques em relação à origem: Torque 1 tem módulo de 2,0 N.m e aponta no sentido positivo do eixo x; Torque 2 tem módulo de 4,0 N.m e aponta no sentido negativo do eixo y. Determine dL/dt, onde L é o momento angular da partícula em relação à origem, em termos dos vetores unitários.

4> Duas patinadoras com 50 kg de massa, que se movem com velocidade escalar de 1,4 m/s, se aproximam em trajetórias paralelas separadas por 3,0 m. Uma das patinadoras carrega uma vara comprida, de massa desprezível, segurando-a em uma extremidade, e a outra se agarra à outra extremidade ao passar pela vara, o que faz com que as patinadoras passem a descrever uma circunferência em torno do centro da vara. Suponha que o atrito entre entre as patinadoras e o gelo é desprezível. Qual é (a) o raio da circunferência, (b) a velocidade angular das patinadoras, (c) a energia cinética do sistema das duas patinadoras? Em seguida, as patinadoras puxam a vara até ficarem separadas por uma distância de 1,0 m. Nesse instante, qual é (d) a velocidade angular das patinadoras e (e) a energia cinética do sistema? (f) De onde vem a energia cinética adicional?

5> Uma barata de massa 0,17 kg corre no sentido anti-horário na borda de um disco circular de raio 15 cm e momento de inércia 5,0 x 10ˆ-3 kg . mˆ2, montado em um eixo vertical com atrito desprezível. A velocidade da barata (em relação ao chão) é de 2,0 m/s e o disco gira no sentido horário com uma velocidade angular de 2,8 rad/s. A barata encontra uma migalha de pão na borda e, obviamente, para. Qual é a velocidade angular do disco depois que a barata para?

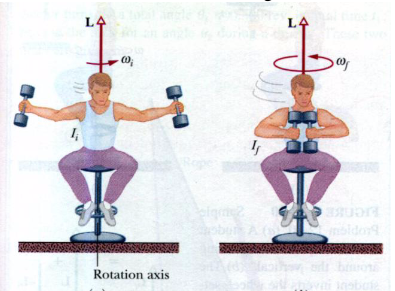
Aula 5 - Dinâmica de Rotação - Parte Final

 Começaremos a aula recordando o que vimos na semana anterior.  Depois de resolver exercício de recordação falaremos sobre a 2ª Lei de Newton para as rotações.

A seguir discutiremos o Princípio de Conservação do Momento Angular.

Terminaremos com exercícios e falando da prova que ocorrerá na próxima semana.

Leis de Kepler

Aula

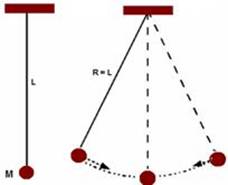
Aula 4 - Laboratório

Utilização do Pêndulo Simples para determinação da Aceleração da Gravidade Local:

No início, resolveremos um exercício da última aula, logo depois faremos o laboratório.

Determinação do Período de Oscilação de um pêndulo simples:

Isolar g, medir L e T e determinar a aceleração da gravidade local. Repetir o procedimento três vezes com tamanhos diferentes de pêndulos.

Roteiro - Taubaté

Aula 3 - Exercícios de Sala

 1> A figura 10-31a mostra um disco que pode girar em torno de um eixo perpendicular à sua face a uma distância h do centro do disco. A figura 10-31b mostra o momento de inércia I do disco em relação ao eixo em função da distância h, do centro até a borda do disco. A escala do eixo I é definida por I(A) = 0,050 kg . mˆ2 e I (B) = 0,150 kg . mˆ2. Qual é a massa do disco?

2> Calcule o momento de inércia de uma régua de um metro, com uma massa de 0,56 kg, em relação a um eixo perpendicular à régua na marca de 20 cm. (Trate a régua como uma barra fina.) 

3> O corpo da figura 10-36 pode girar em torno de um eixo perpendicular ao papel passando por O e está submetido a duas forças, como mostra a figura. Se r1 = 1,30 m, r2 = 2,15 m, F1 = 4,20 N, F2 = 4,90 N, teta1 = 75,0º e teta2 = 60,0º, qual é o torque resultante em relação ao eixo?

4> Uma pequena bola de massa 0,75 kg está presa a uma das extremidades de uma barra de 1,25 m de comprimento e massa desprezível. A outra extremidade da barra está pendurada em um eixo. Qual é o módulo do torque exercido pela força gravitacional em relação ao eixo quando o pêndulo assim formado faz um ângulo de 30º com a vertical?

5> Se um torque de 32,0 N.m exercido sobre uma roda produz uma aceleração angular de 25,0 rad/sˆ2, qual é o momento de inércia da roda?

6> Na figura, o bloco 1 tem massa m1 = 460g, o bloco 2 tem massa m2 = 500g, e a polia, que está montada em um eixo horizontal com atrito desprezível, tem um raio R = 5,00 cm. Quando o sistema é liberado a partir do repouso, o bloco 2 cai 75,0 cm em 5,00 sem que a corda deslize na borda da polia. (a) Qual é o módulo da aceleração dos blocos? (b) Qual é o valor da Tensão T2 e (c) da Tensão T1? (d) Qual é o módulo da aceleração angular da polia? (e) Qual é o momento de inércia da polia?

Aula 3 - Dinâmica de Rotação

Aula 3

Falaremos do Teorema dos Eixos Paralelos. Teorema que nos mostra como calcular o Momento de Inércia em um eixo paralelo ao Centro de Massa:

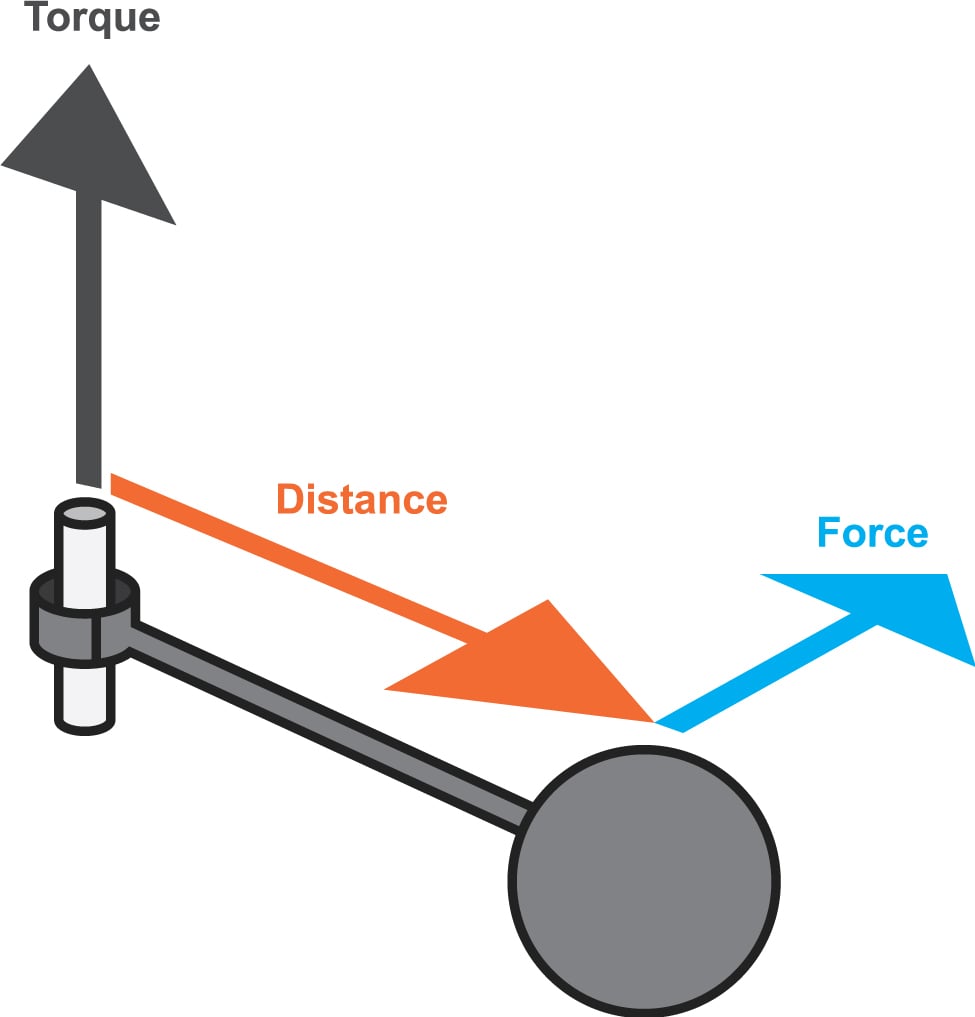
Em nossa 3ª aula, passaremos a falar do conceito de Momento de uma Força - Torque. Faremos a relação do conceito com o que aprendemos anteriormente.

Vídeo Introdutório para entendermos Torque

Aula sobre Torque na Unicamp

No final da aula iremos discutir sobre Equilíbrio de Rotação dos Corpos Rígidos. Estaremos discutindo problemas como:

Explicando Torque e Dinâmica de Rotação

Universo Mecânico:

Aula 2 - Exercícios de Sala

1> Calcule o momento de inércia de uma roda que possui uma energia cinética de 24 400 J quando gira 602 rev/min.

2> A figura 10-31a mostra um disco que pode girar em torno de um eixo perpendicular à sua face a uma distância h do centro do disco. A figura 10-31b mostra o momento de inércia I do disco em relação ao eixo em função da distância h, do centro até a borda do disco. A escala do eixo I é definida por I(A) = 0,050 kg . mˆ2 e I (B) = 0,150 kg . mˆ2. Qual é a massa do disco?

3> Calcule o momento de inércia de uma régua de um metro, com uma massa de 0,56 kg, em relação a um eixo perpendicular à régua na marca de 20 cm. (Trate a régua como uma barra fina.)

Aula 2 - Energia Cinética de Rotação e Momento de Inércia

Aula 2:

 

Iniciaremos falando de Cinemática Angular.

Após isso definiremos a energia cinética de rotação e introduziremos o conceito de Momento de Inércia.

Momento de Inércia de alguns Sólidos

Falaremos, também, do Teorema dos Eixos Paralelos. Teorema que nos mostra como calcular o Momento de Inércia em um eixo paralelo ao Centro de Massa:

Aula da Unicamp de Cinemática de Rotação

Simulador Phet

https://phet.colorado.edu/pt_BR/simulation/legacy/rotation

Outros Simuladores:

http://plato.if.usp.br/2-2003/fap0153d/applets/rotacoes.html

Iniciação Tecnológica - Carrinho com Ratoeira

 Regras – Carrinho com Ratoeira

1> A equipe deverá ser formada de até 4 elementos.

2> Construa um veículo que se desloque o mais rápido possível uma distância de 3 m, quando a mola da ratoeira é liberada.

3> A ratoeira deve ser parte do carro e mover-se junto com ele.

4> Você poderá usar apenas uma ratoeira.

5> Nenhum outro meio de propulsão é permitido.

6> A competição ocorrerá como corrida de arrancada. Teremos duas pistas de 3 m por 90 cm.

7> Para liberação do carrinho na largada, você deverá ter um sistema remoto. Você não poderá ter contato físico direto com a ratoeira (pode ser um bastão para tocar na mesma).

8> No caso de o carrinho queimar a linha demarcatória da pista ele será desclassificado naquele ponto. Caso os dois queimem, vence o carrinho que queimou mais próximo da linha de chegada.

9> Chassis, rodas e eixos, podem ser feitos de qualquer tipo de material, desde que não sejam perigosos.

10> A ratoeira deverá ter no máximo (base) 12cm x 7 cm. A haste de liberação e o engate não poderão ser modificados.

11> Casos omissos nas regras serão decididos pela comissão julgadora. A comissão julgadora é o professor.

RELATÓRIO

1> Nome dos Elementos do Grupo

2> Projeto (dimensões – Foto ou desenho)

3> Física da disciplina envolvida no projeto – Relação

4> Problemas e Soluções

5> Conclusão

6> Referências