1> Uma partícula sofre ação de dois torques em relação à origem: Torque 1 tem módulo de 2,0 N.m e aponta no sentido positivo do eixo x; Torque 2 tem módulo de 4,0 N.m e aponta no sentido negativo do eixo y. Determine dL/dt, onde L é o momento angular da partícula em relação à origem, em termos dos vetores unitários.
quinta-feira, 23 de setembro de 2021
Aula 6 - Exercícios de Sala
Aula 6 - Dinâmica de Rotação - Parte Final
Começaremos a aula recordando o que vimos na semana anterior. Depois de resolver exercício de recordação falaremos sobre a 2ª Lei de Newton para as rotações.
sábado, 11 de setembro de 2021
Aula 5 - Laboratório Presencial
Nossa aula 5 será realizada presencialmente, aqueles que não puderem, poderão acessar o Teams da mesma forma e acompanhar o laboratório de casa.
Link para quem vai ficar em casa
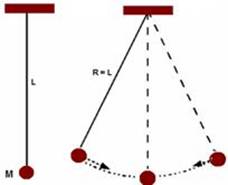
Utilização do Pêndulo Simples para determinação da Aceleração da Gravidade Local:
sexta-feira, 10 de setembro de 2021
Atividade da Aula 4
Após terminar a atividade, favor enviar pelo e-mail ruvlemes@anhanguera.com. Pode ser uma foto da folha onde você fez. Se enviar até o final da aula, confirmar a chegada do e-mail com o professor.
1> Quais são as condições para a existência do equilíbrio estático em corpos rígidos?
2> O produto vetorial entre dois vetores sempre resultará um vetor com qual direção?
3> Explique, com suas palavras, a grandeza momento angular.
4> Cite exemplo de momento angular.
5> Resolva o produto vetorial a x b; onde a = 3j - 5k e b = - 6i + 10j.
Aula 4 - Exercícios de Sala
1> Em termos dos vetores unitários, qual é o torque resultante em relação à origem a que está submetida uma pulga localizada nas coordenadas (0; -4,0 m; 5,0 m) quando as forças F1 = 3 k (N) e F2 = - 2 j (N) agem sobre a pulga?
Aula 4 - Equilíbrio de Corpos Rígidos e Momento Angular
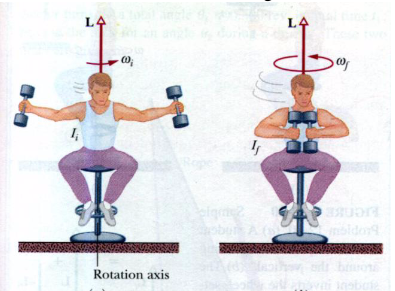
Em nossa aula 4 o assunto principal é o Momento Angular. Momento Angular é uma grandeza similar ao momento linear para o mundo das rotações.
sexta-feira, 3 de setembro de 2021
Laboratório Virtual
Acessar o Lab Virtual:
https://phet.colorado.edu/pt_BR/simulations/pendulum-lab
Entregar
L = ...... m
Tabela