Aula 6 - 2ª Lei das Rotações - Conservação do Momento Angular e Equilíbrio de Corpos Rígidos

Prezados alunos nessa semana teremos aula online no horário normal de aula, abaixo você encontrará o link para essas aulas. Apenas lembrando que para turma de Taubaté a aula será na segunda-feira às 19h20min e para turma de Pindamonhangaba a aula será na quarta-feira às 19h10min.

Link para Taubaté

Aula - Taubaté

Link para Pindamonhangaba

Aula - Pinda

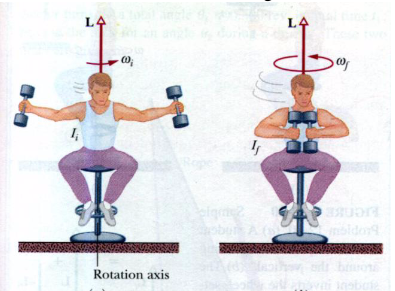
A aula começará falando de Momento angular, em termos de seu módulo:

L = I . w

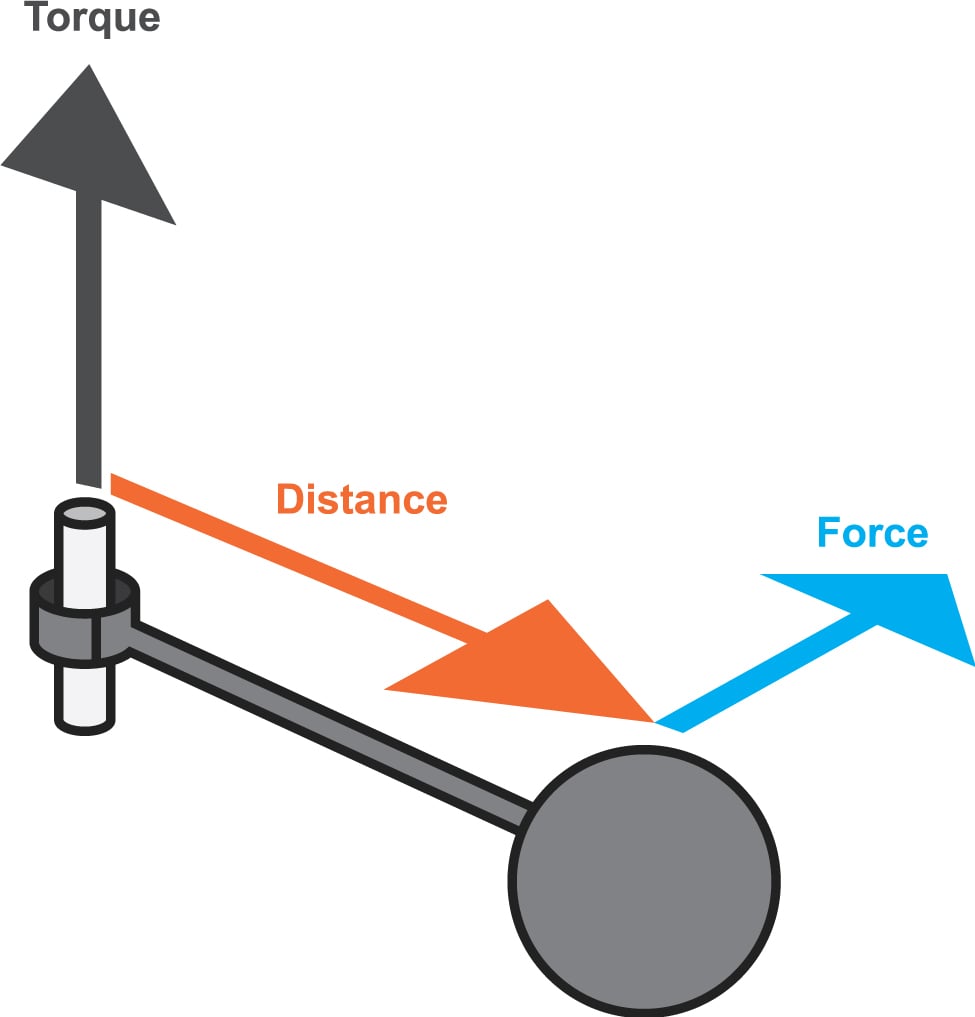
Passando a discutir a 2ª Lei de Newton para as rotações.

A seguir discutiremos o Princípio de Conservação do Momento Angular.

Terminaremos com o assunto de equilíbrio do corpo rígido, fechando as duas primeiras unidades do nosso semestre.

Fique de olho nos exercícios publicados antes deste post, pois eles serão discutidos em nossa aula.

Leis de Kepler

Exercícios de Sala da Aula 6

1> Uma partícula sofre ação de dois torques em relação à origem: Torque 1 tem módulo de 2,0 N.m e aponta no sentido positivo do eixo x; Torque 2 tem módulo de 4,0 N.m e aponta no sentido negativo do eixo y. Determine dL/dt, onde L é o momento angular da partícula em relação à origem, em termos dos vetores unitários.

2> Duas patinadoras com 50 kg de massa, que se movem com velocidade escalar de 1,4 m/s, se aproximam em trajetórias paralelas separadas por 3,0 m. Uma das patinadoras carrega uma vara comprida, de massa desprezível, segurando-a em uma extremidade, e a outra se agarra à outra extremidade ao passar pela vara, o que faz com que as patinadoras passem a descrever uma circunferência em torno do centro da vara. Suponha que o atrito entre entre as patinadoras e o gelo é desprezível. Qual é (a) o raio da circunferência, (b) a velocidade angular das patinadoras, (c) a energia cinética do sistema das duas patinadoras? Em seguida, as patinadoras puxam a vara até ficarem separadas por uma distância de 1,0 m. Nesse instante, qual é (d) a velocidade angular das patinadoras e (e) a energia cinética do sistema? (f) De onde vem a energia cinética adicional?

3> Uma barata de massa 0,17 kg corre no sentido anti-horário na borda de um disco circular de raio 15 cm e momento de inércia 5,0 x 10ˆ-3 kg . mˆ2, montado em um eixo vertical com atrito desprezível. A velocidade da barata (em relação ao chão) é de 2,0 m/s e o disco gira no sentido horário com uma velocidade angular de 2,8 rad/s. A barata encontra uma migalha de pão na borda e, obviamente, para. Qual é a velocidade angular do disco depois que a barata para?

Importante - Trabalhos de Iniciação Tecnológica - Troca

Caros Alunos o trabalho de Iniciação Tecnológica está suspenso. Para efetivarmos a avaliação dos mesmos, segue abaixo uma lista de questões que devem ser respondidas e enviadas para meu e-mail. O prazo de entrega deve ser até o dia 02 de abril. As respostas devem ter coerência e lógica, não se preocupem em copiar de algum lugar, mas de serem honestos com o que vocês sabem e aprenderam.

Lista de Questões

1> Quando medimos o momento de Inércia de uma peça, o que estamos medindo na prática?

2> Força aplicada sobre um corpo prova translação no mesmo. O que devemos aplicar no corpo para provocar rotação?

3> Para transformarmos uma grandeza escalar em angular, o que devemos fazer?

4> Uma patinadora artística, controla a velocidade de seu giro com seus braços, o que ela faz para ganhar velocidade? E o que ela faz para diminuir a sua velocidade? Qual grandeza física ela está modificando com esses movimentos?

5> Qual o período e a frequência (em s e Hz) do movimento de rotação da Terra?

6> Resolva o produto vetorial a x b, onde a = 3i - 4j e b = - 5j + 3k.

Basta enviar uma foto da folha resolvida para ruvlemes@anhanguera.com

Fico no aguardo.

Não desanime, vamos seguindo no estudo! 

Aula 5 - Exercícios de Sala

1> Em termos dos vetores unitários, qual é o torque resultante em relação à origem a que está submetida uma pulga localizada nas coordenadas (0; -4,0 m; 5,0 m) quando as forças F1 = 3 k (N) e F2 = - 2 j (N) agem sobre a pulga?

2> Em um certo instante, a força F = 4,0 j (N) age sobre um objeto de 0,25 kg cujo vetor posição é r = (2,0 i - 2,0 k)  m e cujo vetor velocidade é v = (-5,0 i + 5,0 k) m/s. Em relação à origem e em termos dos vetores unitários, qual é (a) o momento angular do objeto e (b) o torque que age sobre o objeto?

3> Um objeto de 2,0 kg, que se comporta como uma partícula se move em um plano com componentes de velocidade vx = 30 m/s e vy = 60 m/s ao passar por um ponto de coordenadas (3,0; -4,0)m. Nesse instante, em termos dos vetores unitários, qual é o momento angular do objeto em relação (a) à origem e (b) ao ponto (-2,0; -2,0) m?

Aula 5 - Momento Angular

Caros alunos, peço por favor, que coloquem o nome, curso e unidade (cidade) no comentário deste post para que eu possa saber quais alunos assistiram a aula. Agradeço a atenção.


Em nossa aula 5 o assunto principal é o Momento Angular. Momento Angular é uma grandeza similar ao momento linear para o mundo das rotações.

Para entender essas grandezas é necessário recorda o produto vetorial

Produto Vetorial:

Regra da Mão Direita:

Exemplo de Produto Vetorial

Discutindo de forma rápida as grandezas Vetor Torque e Momento Angular:

Momento Angular - Universo Mecânico

Aula sobre Momento Angular na Unicamp:

Harmonia dos Mundos - Cosmos

Lendo Sobre Kepler

Importante

Caros alunos neste momento difícil que todos nós passamos é de extrema importância que primeiramente se cuidem. Além disso para o seguimento do curso é fundamental que desenvolvam as atividades do AVA - Unidade I e Unidade II. Continuem acompanhando as aulas no AVA e aqui no Blog. 

Qualquer dúvida: ruvlemes@anhanguera.com

Regras do Carrinho de Ratoeira - Relatório

Regras – Carrinho com Ratoeira

1> A equipe deverá ser formada de até 4 elementos.

2> Construa um veículo que se desloque o mais rápido possível uma distância de 5 m, quando a mola da ratoeira é liberada.

3> A ratoeira deve ser parte do carro e mover-se junto com ele.

4> Você poderá usar apenas uma ratoeira.

5> Nenhum outro meio de propulsão é permitido.

6> A competição ocorrerá como corrida de arrancada. Termos duas pistas de 5 m por 90 cm.

7> Para liberação do carrinho na largada, você deverá ter um sistema remoto. Você não poderá ter contato físico direto com a ratoeira (pode ser um bastão para tocar na mesma).

8> No caso de o carrinho queimar a linha demarcatória da pista ele será desclassificado naquele ponto. Caso os dois queimem, vence o carrinho que queimou mais próximo da linha de chegada.

9> Chassis, rodas e eixos, podem ser feitos de qualquer tipo de material, desde que não sejam perigosos.

10> A ratoeira deverá ter no máximo (base) 12cm x 7 cm. A haste de liberação e o engate não poderão ser modificados.

11> Casos omissos nas regras serão decididos pela comissão julgadora. A comissão julgadora é o professor.

RELATÓRIO

1> Nome dos Elementos do Grupo

2> Projeto (dimensões – Foto ou desenho)

3> Física da disciplina envolvida no projeto – Relação

4> Problemas e Soluções

5> Conclusão

6> Referências

Exercícios de Sala - Aula 4

1> O corpo da figura 10-36 pode girar em torno de um eixo perpendicular ao papel passando por O e está submetido a duas forças, como mostra a figura. Se r1 = 1,30 m, r2 = 2,15 m, F1 = 4,20 N, F2 = 4,90 N, teta1 = 75,0º e teta2 = 60,0º, qual é o torque resultante em relação ao eixo?

2> Uma pequena bola de massa 0,75 kg está presa a uma das extremidades de uma barra de 1,25 m de comprimento e massa desprezível. A outra extremidade da barra está pendurada em um eixo. Qual é o módulo do torque exercido pela força gravitacional em relação ao eixo quando o pêndulo assim formado faz um ângulo de 30º com a vertical?

3> Se um torque de 32,0 N.m exercido sobre uma roda produz uma aceleração angular de 25,0 rad/sˆ2, qual é o momento de inércia da roda?

4> Na figura, o bloco 1 tem massa m1 = 460g, o bloco 2 tem massa m2 = 500g, e a polia, que está montada em um eixo horizontal com atrito desprezível, tem um raio R = 5,00 cm. Quando o sistema é liberado a partir do repouso, o bloco 2 cai 75,0 cm em 5,00 sem que a corda deslize na borda da polia. (a) Qual é o módulo da aceleração dos blocos? (b) Qual é o valor da Tensão T2 e (c) da Tensão T1? (d) Qual é o módulo da aceleração angular da polia? (e) Qual é o momento de inércia da polia?

Aula 4 - Dinâmica de Rotação

Falaremos do Teorema dos Eixos Paralelos. Teorema que nos mostra como calcular o Momento de Inércia em um eixo paralelo ao Centro de Massa:

Em nossa 4ª aula, passaremos a falar do conceito de Momento de uma Força - Torque. Faremos a relação do conceito com o que aprendemos anteriormente.

Vídeo Introdutório para entendermos Torque

Aula sobre Torque na Unicamp

No final da aula iremos discutir sobre Equilíbrio de Rotação dos Corpos Rígidos. Estaremos discutindo problemas como:

Explicando Torque e Dinâmica de Rotação

Universo Mecânico:

Aula 3 - Laboratório - Determinação da Aceleração da Gravidade Local e Centro de Massa

Pindamonhangaba - 11/03

Taubaté - 16/03

Utilização do Pêndulo Simples para determinação da Aceleração da Gravidade Local:

Determinação do Período de Oscilação de um pêndulo simples:

Isolar g, medir L e T e determinar a aceleração da gravidade local. Repetir o procedimento três vezes com tamanhos diferentes de pêndulos.

A 2ª parte do laboratório é fazendo uso do centro de equilíbrio determinar o centro de massa de algumas figuras geométricas conhecidas.

Roteiro - Taubaté

Roteiro - Pinda