Laboratório - Turma de Taubaté

Na Turma de Taubaté noturno teremos nessa semana mais um laboratório. Abaixo vocês encontram o roteiro que deve ser levado para uso da equipe.

Roteiro de Taubaté

Aula 5 - Pós Aula

Após nossa Aula 5 você deve saber responder as seguintes questões:

1> O produto vetorial sempre fornece um vetor. Qual a direção, desse vetor, em relação aos vetores que lhe deram origem?

2> Momento Angular pode ser escrito a partir do momento linear, como você definiria essas duas grandezas?

3> Qual o produto vetorial de:

(a) i x i; (b) i x j; (c) i x k; (d) j x j; (e) j x i; (f) j x k; (g) k x k; (h) k x i; (i) k x j.

4> Por que utilizamos a letra L para Momento Angular?

(Desafio do dia)

5> Dê um exemplo no dia a dia de Momento Angular.

Aula 5 - Exercícios de Sala

1> Em termos dos vetores unitários, qual é o torque resultante em relação à origem a que está submetida uma pulga localizada nas coordenadas (0; -4,0 m; 5,0 m) quando as forças F1 = 3 k (N) e F2 = - 2 j (N) agem sobre a pulga?

2> Em um certo instante, a força F = 4,0 j (N) age sobre um objeto de 0,25 kg cujo vetor posição é r = (2,0 i - 2,0 k)  m e cujo vetor velocidade é v = (-5,0 i + 5,0 k) m/s. Em relação à origem e em termos dos vetores unitários, qual é (a) o momento angular do objeto e (b) o torque que age sobre o objeto?


3> Um objeto de 2,0 kg, que se comporta como uma partícula se move em um plano com componentes de velocidade vx = 30 m/s e vy = 60 m/s ao passar por um ponto de coordenadas (3,0; -4,0)m. Nesse instante, em termos dos vetores unitários, qual é o momento angular do objeto em relação (a) à origem e (b) ao ponto (-2,0; -2,0) m?

Aula 5 - Momento Angular

Em nossa aula 5 falaremos sobre o Momento Angular. Momento Angular é uma grandeza similar ao momento linear para o mundo das rotações.

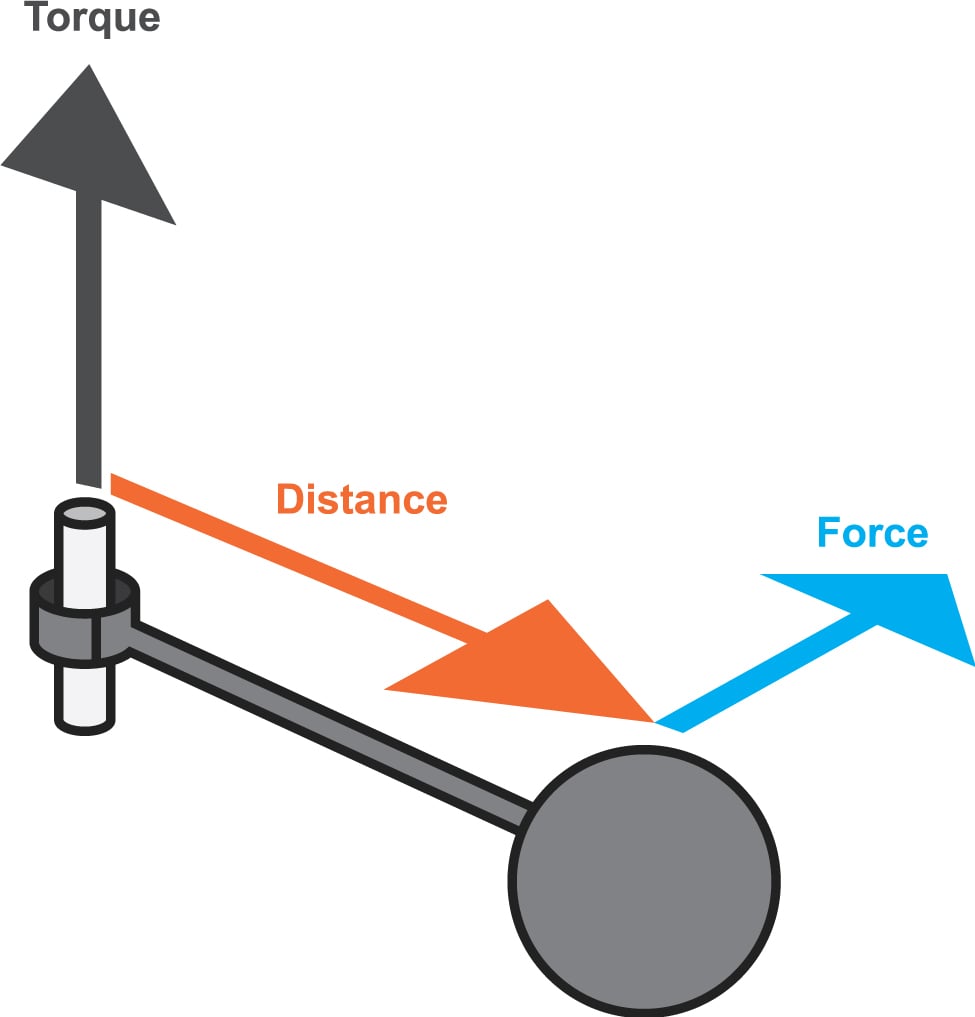
O conceito de produto vetorial é muito importante neste momento do curso, pois é marcante na definição de Torque e Momento Angular.

Produto Vetorial:

Regra da Mão Direita:

Torque:

τ = r × F

Momento Angular:

L = m ( r x v)

Aula sobre Momento Angular na Unicamp:

Momento Angular - Universo Mecânico

Harmonia dos Mundos - Cosmos

Lendo Sobre Kepler

Aula 4 - Pós Aula

Após nossa aula dessa semana o aluno deve ser capaz de responder as seguintes questões:

1> Quais as diferenças entre Torque e Momento de Inércia?

2> Existe uma relação similar para a 2ª Lei de Newton no estudo de movimento de rotação? Qual é?

3> Para que serve o Teorema dos Eixos Paralelos? Faça sua demonstração.

4> Reveja o problema dado em aula:

Aula 4 - Exercícios de Sala

1> O corpo da figura 10-36 pode girar em torno de um eixo perpendicular ao papel passando por O e está submetido a duas forças, como mostra a figura. Se r1 = 1,30 m, r2 = 2,15 m, F1 = 4,20 N, F2 = 4,90 N, teta1 = 75,0º e teta2 = 60,0º, qual é o torque resultante em relação ao eixo?

2> Uma pequena bola de massa 0,75 kg está presa a uma das extremidades de uma barra de 1,25 m de comprimento e massa desprezível. A outra extremidade da barra está pendurada em um eixo. Qual é o módulo do torque exercido pela força gravitacional em relação ao eixo quando o pêndulo assim formado faz um ângulo de 30º com a vertical?

3> Se um torque de 32,0 N.m exercido sobre uma roda produz uma aceleração angular de 25,0 rad/sˆ2, qual é o momento de inércia da roda?

4> Na figura, o bloco 1 tem massa m1 = 460g, o bloco 2 tem massa m2 = 500g, e a polia, que está montada em um eixo horizontal com atrito desprezível, tem um raio R = 5,00 cm. Quando o sistema é liberado a partir do repouso, o bloco 2 cai 75,0 cm em 5,00 sem que a corda deslize na borda da polia. (a) Qual é o módulo da aceleração dos blocos? (b) Qual é o valor da Tensão T2 e (c) da Tensão T1? (d) Qual é o módulo da aceleração angular da polia? (e) Qual é o momento de inércia da polia?

Aula 4 - Teorema dos Eixos Paralelos e Dinâmica de Rotação

Em nossa 4ª aula, iniciaremos falando do Teorema dos Eixos Paralelos. Teorema que nos mostrará como calcular o Momento de Inércia em um eixo paralelo ao Centro de Massa:

Passaremos a falar do conceito de Momento de uma Força - Torque. Faremos a relação do conceito com o que aprendemos anteriormente.

Vídeo Introdutório para entendermos Torque

Aula sobre Teorema dos eixos paralelos e Torque na Unicamp

No final da aula iremos discutir sobre Equilíbrio de Rotação dos Corpos Rígidos. Estaremos discutindo problemas como:

Universo Mecânico:

Aula 3 - Laboratório - Pós Aula

Após o Laboratório da aula 3 você deve ser capaz de responder:

1> Como você procedeu para determinar o centro de massa das figuras geométricas?

2> O que ocorre com a aceleração da gravidade quando medida em cidades de altitudes diferentes?

3> Qual a relação do período de um pêndulo simples?

4> Por que devemos iniciar o movimento pendular com ângulo pequeno?

5> O valor encontrado pelo seu grupo foi dentro do esperado? Justifique.

6> Cite três situações físicas em que a aceleração da gravidade é de extrema importância.

Aula 3 - Laboratório

Para conhecer mais detalhes sobre a determinação da aceleração da gravidade local leia o seguinte artigo:

http://www.iag.usp.br/~eder/EAD/aula5.pdf

A gravimetria é de grande importância, veja:

http://www.iag.usp.br/siae98/geofisica/geofmetodos.htm

Abaixo você possui a foto de um gravímetro:

Aula 3 - Laboratório Centro de Massa e Determinação da Aceleração da Gravidade Local

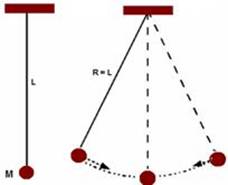
Utilização do Pêndulo Simples para determinação da Aceleração da Gravidade Local:

Determinação do Período de Oscilação de um pêndulo simples:

Isolar g, medir L e T e determinar a aceleração da gravidade local. Repetir o procedimento três vezes com tamanhos diferentes de pêndulos.

A 2ª parte do laboratório é fazendo uso do centro de equilíbrio determinar o centro de massa de algumas figuras geométricas conhecidas.

Roteiro de Taubaté:

Roteiro

Roteiro de Pindamonhangaba:

Roteiro

Roteiro de Jacareí:

Roteiro

Aula 2 - Pós Aula

Após nossa 2ª semana de aula você deve ser capaz de resolver:

1> Suponhamos um conjunto de três bastões rígidos de 4 m de comprimento e massa desprezível, mas muito resistentes. Os chamaremos de bastões A, B e C. Eles são presos pelo centro em um eixo que gira com velocidade angular constante. Neles, conforme figura (dada em aula), em primeiro lugar são inseridos 6 kg de massa em cada extremidade do bastão A. Em segundo lugar, inserimos 3,0 kg em cada ponta, e mais 3,0 kg entre a extremidade e o eixo de giro no bastão B. Por fim, inserimos 2 kg nas extremidades e 2 kg a cada terço da distância até o eixo de rotação do bastão C. Percebam que, após fazer isso, colocando cada um dos três bastões em uma balança, temos a mesma leitura de massa total: 12 kg. Calcule o Momento de Inércia em cada caso.

Respostas: A => 48 kg mˆ2; B => 30 kg mˆ2; C => 24,86 kg mˆ2 


2> A . posição angular de um ponto de uma roda é dada por: teta = 3,0 - 4,0 t + 6 t³, onde teta está em radianos e t em segundos. Determine o que é pedido abaixo:

(a) a posição angular em t = 5 s;

(b) a função da velocidade angular;

(c) a função da aceleração angular;

(d) a velocidade angular é constante?

Respostas: (a) 733 rad; (b) w = - 4 + 18 tˆ2; (c) alfa = 36 t; (d) não.

Aula 2 - Exercícios de Sala

1> Qual é a velocidade angular (a) do ponteiro dos segundos, (b) do ponteiro de minutos e (c) do ponteiro de horas de um relógio analógico? Dê as respostas em radianos por segundo.

2> A posição angular de um ponto de uma roda é dado por: teta = 2 + 4tˆ2 + 3tˆ3, onde teta está em radianos e t em segundos. Em t = 0, qual é (a) a posição e (b) a velocidade angular do ponto? (c) Qual é a velocidade angular em t = 4s? (d) Calcule a aceleração angular em t = 2 s. (e) A aceleração angular da roda é constante?

3> Um disco, inicialmente girando a 120 rad/s, é freado com uma aceleração angular constante de módulo 4 rad/sˆ2. (a) Quanto tempo o disco leva para parar? (b) Qual é o ângulo total descrito pelo disco durante esse tempo?

4> Calcule o momento de inércia de uma roda que possui uma energia cinética de 24 400 J quando gira 602 rev/min.

5> A figura 10-31a mostra um disco que pode girar em torno de um eixo perpendicular à sua face a uma distância h do centro do disco. A figura 10-31b mostra o momento de inércia I do disco em relação ao eixo em função da distância h, do centro até a borda do disco. A escala do eixo I é definida por I(A) = 0,050 kg . mˆ2 e I (B) = 0,150 kg . mˆ2. Qual é a massa do disco?

Exercícios retirados do livro Fundamentos da Física (Halliday)

Aula 2 - Energia Cinética de Rotação e Momento de Inércia

Em nossa 2ª aula terminaremos a discussão sobre grandezas angulares e as relacionaremos com as grandezas escalares.  A seguir definiremos o Movimento Circular Uniforme (MCU).

Após isso definiremos a energia cinética de rotação e introduziremos o conceito de Momento de Inércia.

Momento de Inércia de alguns Sólidos

Aula da Unicamp de Cinemática de Rotação

Simulador Phet

https://phet.colorado.edu/pt_BR/simulation/legacy/rotation

Outros Simuladores:

http://plato.if.usp.br/2-2003/fap0153d/applets/rotacoes.html

Ressonância - Ponte de Tacoma

Comentado em sala de aula:

Aula 1 - Centro de Massa - Pós Aula

Após a nossa primeira aula o aluno deverá ser capaz de responder as seguintes questões:

1> Qual a importância do estudo da física de rotações para o nosso dia a dia?

2> O que é o centro de massa de um corpo?

3> Como determinamos as coordenadas do centro de massa de um corpo?

4> O que é 1 radiano?

Iniciação Tecnológica - Carrinho com Ratoeira

As regras da competição você encontra no arquivo abaixo:

Regras

Aula 1 - Critérios - Disciplina - Centro de Massa

Em nossa primeira aula explicaremos o PEA, falaremos dos critérios de avaliação e como será nosso 2º Semestre.

Critérios de Avaliação

1º Bimestre

Prova - 0 a 10,0 (70%)

Iniciação Tecnológica - 0 a 7,0
Carrinho com Ratoeira
Laboratório - 0 a 3,0

2º Bimestre

Prova - 0 a 10,0 (70%)

Iniciação Tecnológica - 0 a 7,0
Guindaste Hidráulico
Laboratório - 0 a 3,0

OBS: Existe a possibilidade de extras (3 primeiros das IT's)

Meu email: ruvlemes@anhanguera.com

O que estudaremos em Física Geral Experimental: Energia ?

• Rotação dos Corpos Rígidos
• Dinâmica do Movimento de Rotação
• Mecânica dos Fluidos
• Temperatura e Calor

Em nossa primeira aula iniciaremos falando do Centro de Massa de um sistema de partículas.

A seguir falaremos sobre grandezas angulares: posição angular, velocidade angular, aceleração angular. Relacionaremos as grandezas escalares com as grandezas angulares. Introduziremos o conceito de Movimento Circular Uniforme, suas equações e possíveis generalizações.

Grandes Descobertas na Astronomia